Home 문제로 풀어보는 알고리즘 00장
Post
Cancel

문제로 풀어보는 알고리즘 00장

Posted 2022-04-01 Updated 2022-04-06 44 min read

최댓값과 최솟값

두 수를 받고 최대/최소를 반환하는 함수

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

int max(int x, int y)
{
    if (x > y)
    {
        return x;
    }
    return y;
}

int min(int x, int y)
{
    if (x < y)
    {
        return x;
    }
    return y;
}

매크로 함수 작성

매크로 함수란? #define으로 함수를 미리 정의해두는 방법을 말한다. 주로 짧고 단순한, 많이 쓰이고 직관적인 구조를 취하는 함수는 매크로 함수로 정의한다.

삼항 연산자에 대하여 if (cond) A else B와 같은 코드는 삼항 연산자로 간단하게 적을 수 있다. : (cond?A:B)

1
2

#define max(x, y) ((x)>(y)?x:y)
#define min(x, y) ((x)<(y)?x:y)

단, 매크로 함수는 그저 글자를 바꿔치기 하는 역할을 하기에 실수할 수 있는 여지가 매우 높다. 매크로 함수를 이용해야하는 특별한 이유가 없다면 보통의 함수로 코드를 작성하자.

세 수를 받고 최대/최소를 반환하는 함수

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

int max(int x, int y, int z)
{
    if (x > y)
    {
        if (x > z)
        {
            return x;
        }
        return z;
    }
    else
    {
        if (y > z)
        {
            return y;
        }
        return z;
    }
}

int max(int x, int y, int z)
{
    if (x < y)
    {
        if (x < z)
        {
            return x;
        }
        return z;
    }
    else
    {
        if (y < z)
        {
            return y;
        }
        return z;
    }
}

배열의 최대값을 구하는 함수

배열을 인자로 전달할 때에는, 포인터 형식으로 준다. 단, 이럴 경우 배열의 길이를 알 수 없기에 배열의 길이 역시 함수의 인자로 전달해야 한다.

배열의 길이는 어떻게 계산할 수 있을까? 많은 방법이 있지만, HARD한 코드로는 sizeof arr / sizeof arr[0]으로 배열의 길이를 계산할 수 있다.

배열이나 문자열을 순회할 때에는 size_t 형식의 인덱스 변수를 선언하는 것이 국룰이다. 하지만 밑의 코드에서는 그냥 int를 썼다. (필자의 숙련도가 부족하니 너그러운 이해를 바란다.) 여담이지만, 위의 sizeof 연산자는 size_t를 반환한다.

1
2
3
4
5
6
7
8
9
10
11
12

int max_arr(int *arr, int n)
{
    int max = arr[0]; // 배열에 완전 탐색 시키면서 최대값을 업데이트 할 것임
    for (int i = 1; i < n; i++) // i가 0부터 시작하지 않는 이유는? 정답은 밑에...
    {
        if (arr[i] > max)
        {
            max = arr[i]; // 순회하고 있는 원소가 기존의 최대값보다 크면 최대값 업데이트
        }
    }
    return max;
}

정답: 이미 max는 arr[0]이므로 밑의 if문을 통과하지 않을 것이 자명하다.

두 변수의 값 바꾸기

포인터를 이용하여 값을 swap하는 함수

main의 변수를 인자로 받을 때 call-by-value 방식을 사용하면 단순히 복사된 값을 사용하기 때문에 메모리도 낭비되고, 원본 값을 수정하지도 못한다. 따라서 많은 경우에 포인터로 인자를 넘기는 call-by-reference를 사용한다.

call-by-reference의 장점은 무엇일까?

  1. main의 원본 변수 값에 접근하여 다이렉트로 수정할 수 있다.
  2. 여러 값을 처리(수정)해야되는 상황에서 유용하다. (이 경우 변수의 포인터를 이용하여 값들만 수정하고, 함수의 반환은 void형식(return ;)이다.)
1
2
3
4
5
6
7
8

void swap(int *a, int *b)
{
    int temp;
    temp = *a;
    *a = *b;
    *b = temp;    
    return ;
}

배열의 두 원소를 swap하는 함수

1
2
3
4
5
6
7
8

void swap_arr(int *arr, int i, int j)
{
    int temp;
    temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;    
    return ;
}

알고 있을 것 같기는 하지만… arr[i]는 *(arr + i)로 처리된다. 즉 결국 [] 연산자는 포인터 연산 + 값 뽑아오기 연산인 셈.

배열 회전

1차원 배열 회전 (오른쪽으로 한 칸)

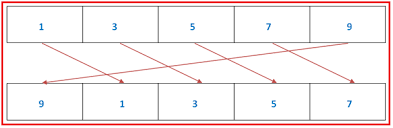rotating-1d-array 1차원 배열 회전 (오른쪽)

1
2
3
4
5
6
7
8
9
10

void right_rotate(int *arr, int s, int t)
{
    int last = arr[t];
    for (int i = t; i > s; i--) // 왜 거꾸로 탐색할까? 밑에 빨간 영역 참고
    {
        arr[i] = arr[i - 1]; // 요게 포인트! 밑에 자세한 설명...
    }
    arr[s] = last;
    return ;
}

설명 : 위와 같은 상황에서, A = B라는 연산자를 바라볼 때 A는 나중 상황, B는 이전 상황으로 볼 수 있다. 즉, 위 그림에서 아래에 있는 배열은 A, 위에 있는 배열은 B인 셈이다. 이것을 먼저 고려한다면, 위 코드를 쉽게 작성할 수 있을 것이다.

이런 식으로 적으면 망한다!

1
2
3
4

for (int i = s; i < t; i++)
{
    arr[i + 1] = arr[i];
}

왜 안 되는지는 스스로 고민해보고 읽기를… 이 코드가 정상적으로 작동하지 않는 이유는, arr[s + 1의 값을 arr[s]로 고친 이후에 arr[s + 2]의 값을 arr[s + 1]로 고치기 때문이다. 즉, 이후에 필요한 변수의 값이 이전에 수정되는, 배열의 모든 원소가 arr[s]가 되는 결과를 초래한다. 필자는 이미 한 번 실수했으니 독자들은 그러지 말기를…

위와 같은 생각을 했지만, 그럴 경우 범위가 애매해진다. 따라서 last라는 변수에 따로 arr[t]를 저장하고, 후에 arr[s]에 대입해주자.

1차원 배열 회전 (왼쪽으로 한 칸)

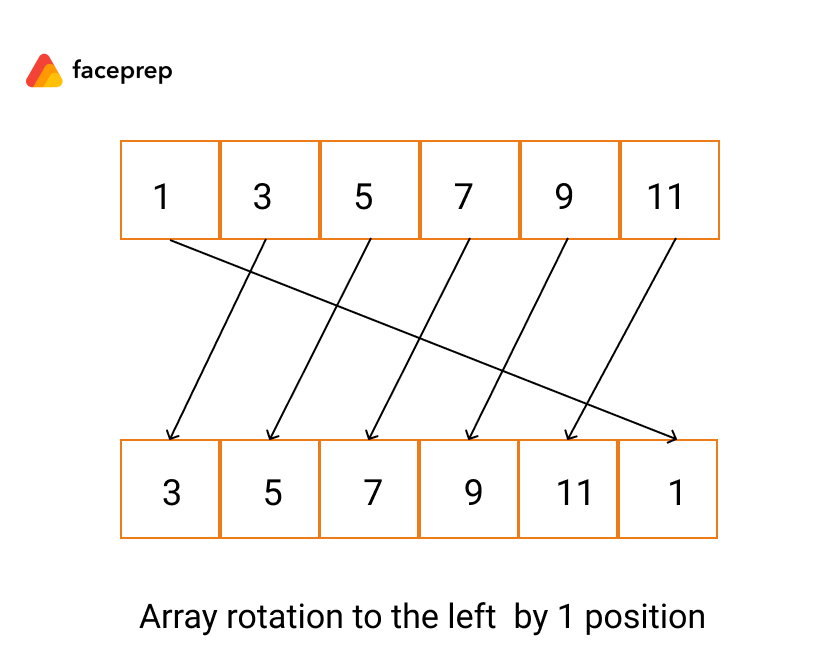rotating-1d-array 1차원 배열 회전 (왼쪽)

1
2
3
4
5
6
7
8
9
10

void left_rotate(int *arr, int s, int t)
{
    int first = arr[s];
    for (int i = s; i < t; i++)
    {
        arr[i] = arr[i + 1];
    }
    arr[t] = first;
    return ;
}

위의 1차원 배열 회전 (오른쪽으로 한 칸)을 참고하면 쉽게 작성할 수 있다. 이때도 마찬가지로 배열의 모든 원소가 한 원소로 덮어써지지 않도록 주의하자.

1차원 배열 회전 (오른쪽으로 k칸)

위의 1차원 배열 회전 (오른쪽으로 한 칸)을 k번 반복하면 되지만, 너무 NAIVE하다.

용어에 익숙치 않은 독자들을 위해 소개하자면, NAIVE하다의 뜻은 순진하다, 무식하다 정도의 뜻이다. (솔직히 무식하게 k번 움직이는 것보다는 더 멋진 코드가 있을 것. 이는 직감적으로 알 수 있음.)

따라서 General한 Form을 찾아보자! 우선 오른쪽으로 한 칸이니까 오른쪽에서 왼쪽으로 배열을 돌아야겠다는 생각이 든다. (이 문장이 이해가 안된다면, 위의 빨간 영역을 다시 읽어보자.)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

void right_rotate_k(int *arr, int s, int t, int k)
{
    int *temp_arr;
    temp_arr = (int *)malloc(k * sizeof(int));
    for (int i = 0; i < k; i++)
    {
        temp_arr[i] = arr[t - k + 1 + i];
    }
    for (int j = t; j >= s + k; j--)
    {
        arr[j] = arr[j - k];
    }
    for (int l = 0; l < k; l++)
    {
        arr[s + l] = temp_arr[l];
    }
    return;
}

우선 k칸만큼 회전할 때 임시적으로 저장해야 하는 놈들은 k개가 된다. 이것을 배열로 저장하자. 사이즈가 달라지므로 동적할당을 사용했다. 동적할당에 대해 모르겠다면 지금은 메모리를 미리 찜해놓는다 정도의 개념으로 알아두자. 중요한 것은 위의 for문과 배열의 index가 왜 저렇게 쓰였는지 정확하게 이해하는 것이다.

은행 대기 번호 관리 (큐/스택)

큐(Queue)는 먼저 들어간 데이터가 먼저 나오는 자료구조를 말한다. (선입선출)

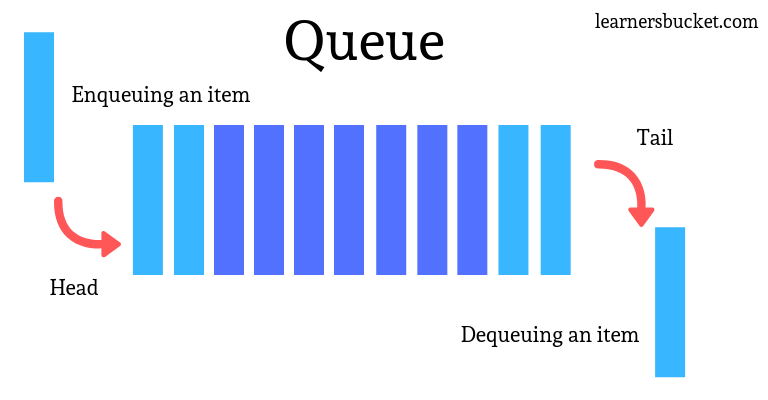queue 큐

큐에 데이터를 넣을 때에는 enqueue라는 용어를 쓰고, 데이터를 뽑아낼 때에는 dequeue라는 용어를 쓴다.

배열로 큐 작성하기

큐를 가장 HARD한 방법으로 코딩하는 방법은, head, tail를 정의하여 배열에서 큐의 컨테이너의 범위를 지정하는 것이다. 쉽게 말해 먼저 들어온 놈을 먼저 내보낼 것인데, 이를 위해 먼저 들어온 놈을 가리키는 index를 변수로 두고 (head), 나중에 들어온 놈을 가리키는 index를 변수로 두는 것이다. (tail)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

int queue[100]; // 왜 배열의 크기를 100개나 잡았을까? 정답은 밑의 빨간 영역에...
int head = 0, tail = 0;

void enqueue(int n) // 값이 큐에 들어옴
{
    if (tail - head == 8) // 큐의 사이즈가 8 이상이면 안 댐!
    {
        cout << "queue is full!" << endl;
        return ;
    }
    queue[tail] = n; // 큐에서 tail의 위치에 입력 데이터 저장
    tail++; // tail 앞으로 한 칸 이동
    return ;
}

int dequeue()
{
    if (tail - head == 0)
    {
        cout << "queue is empty!" << endl;
        return 0;
    }
    int r = queue[head]; // 현재 큐에서 head의 위치에 있는 데이터 반환, 왜 여기서 return을 하지 않았을까? 정답은 설명에...
    head++; // head 앞으로 한 칸 이동
    return r;
}

int main()
{
    int input;
    while (true)
    {
        cin >> input;
        if (input == -1)
        {
            break;
        }
        else if (input == 0)
        {
            cout << dequeue() << endl;
        }
        else if (input > 0)
        {
            enqueue(input);
        }
    }
    return 0;
}

책의 코드는 틀렸다? 그렇다. 책의 코드(28p~29p)는 장의 서문에서 제시한 예시 출력을 반환하지 못한다. 필자가 왜 그런지 열심히 고민해봤는데, 고민의 결과는 다음과 같다.

  • 배열 queue의 크기가 8로 제한되어 있다.
  • 변수 tail의 경우 입력한 횟수만큼 증가한다. (즉, 매우 큰 수가 대입될 수 있다.)
  • 그.런.데! 명령어 queue[tail]이 존재한다. 따라서 이는 배열의 범위보다 큰 인덱스를 처리해야하는 문제로 귀결된다. 필자는 이 문제를 배열 queue의 크기를 나름 큰 크기로 세팅하여 해결하였으나(queue[100]), 입력을 100번 이상 받으면 다시 문제가 발생할 것이다. (즉 queue[k]로 선언했다면 입력을 k번 이상 받을 경우 문제가 발생한다.) 따라서 이 문제를 해결할 멋진 방법을 필요로 하게 된다.

필자는 코드의 일관된 작성을 위하여 인덱스 값을 사용하고 인덱스 값을 업데이트 하는 방식으로 코드를 통일했다. 예컨데 enqueue(int n)와 dequeue()에서

1
2
3

   queue[tail] = n; // 인덱스 값 사용
   tail++; // 인덱스 값 업데이트
   return ;

1
2
3

   int r = queue[head]; // 인덱스 값 사용
   head++; // 인덱스 값 업데이트
   return r;

이렇게 작성한 이유는, 책의 코드 같은 경우 head와 tail을 생성할 때 각각 head = 0, tail = -1과 같이 썼는데, 이렇게 쓸 경우 tail이 -1로 초기화된 것에 대하여 의문점을 가질 수 있고, 무엇보다 직관적이지 못하다.

또 별건 아니지만, 책에서는 queue_size 변수를 따로 만들어서 큐의 크기를 직접 조종하였지만, 위와 같이 일관된 코드를 작성하고 나면 queue_size 변수가 굳이 필요 없다는 것을 알게 된다. 그저 큐의 크기가 필요할 때마다 head - tail로 계산하면 되기 때문이다. 코드의 일관된 작성은 interpretable한 코드를 낼 수 있고, 이는 더 나은 코드를 찾을 수 있다는 점에서 contribution이 있다.

책에 있는 코드에 오타가 있어서 시간을 많이 빼았겨 분하고 화가 나는가? 책의 저자에게 너무 열을 내지 않도록 주의하자. 개발과 관련된 수많은 책의 리뷰를 보다보면, 이따금씩 코드의 오탈자로 저자를 나무라는 분노의 리뷰를 많이 보았다. 하지만 이게 당신의 실력 향상에 도움이 되는가? 전혀 도움 안된다. 물론, 오탈자의 정도가 심하다면 분명 수정이 필요하다. 하지만 코드를 직접 실행해보고, 디버깅해보며, 어떤 코드가 오류를 반환하고, 이를 어떻게 해결할 수 있는지 고민해보는 것도 좋은 공부가 될 것이다. (필자는 위의 빨간 영역을 적으며 많은 것을 배웠다.) 또한 책의 저자는 책의 서문에서 이미 오탈자에 대한 양해를 구하고 있으며, 코드 외적인 부분에서 내용을 훌륭하게 전달하고 있다고 생각한다. 그러니 포기하지 말고, 좀 더 공부해보자. :) (사실 이건 나 자신에게 하는 말과 같다.)

원형 큐 작성하기

배열로 큐 작성하기에서 빨간 영역으로 작성한 배열로 작성한 큐의 한계를 기억하는가? 그것은 바로, 배열 queue[k]로 선언했을 때 입력을 k번 이상 받을 경우 문제가 발생한다는 것이다. 왜냐하면 큐의 끝 인덱스를 나타내는 변수 tail은 입력 횟수에 비례하고, 입력 횟수는 제한이 없기에 배열의 크기보다 큰 인덱스가 들어갈 수 있기 때문이다.

사실 배열로 작성한 큐의 문제는 그뿐만이 아니다. 메모리 효율성의 관점에서 엉망이다. 배열 queue에서 데이터 컨데이너로써 필요한 부분은 인덱스 head ~ tail이 전부이다. 그렇다면 0 ~ head, tail ~ 100은? (queue의 크기가 100이라고 전제하겠다.) 그냥 쓸데없는 부분이다. 이 사용되지도 않을 변수들을 위해서 메모리 상에 미리 자리를 맡아놓아야 한다니, 아깝지 않은가?

이러한 관점에서 고민한 끝에, 새롭게 고안된 데이터 타입이 바로 원형 큐이다.

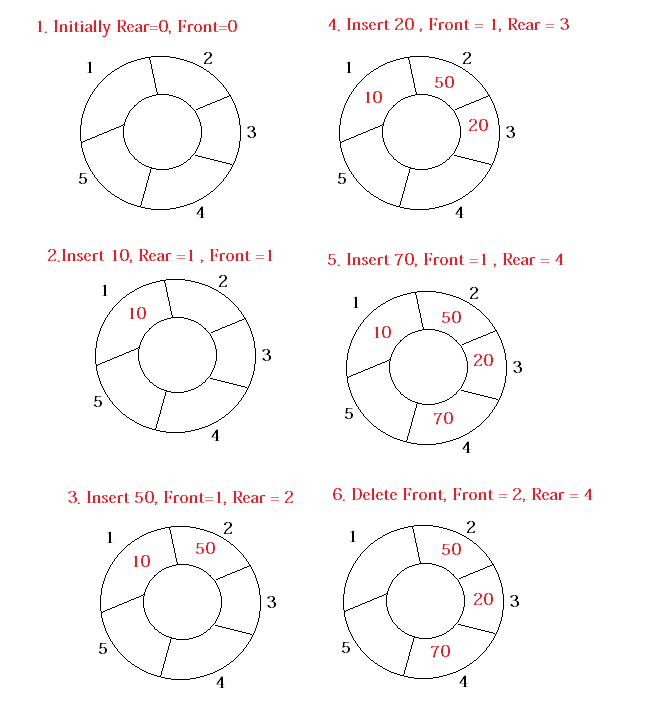circular queue 원형 큐

즉 위에서 구현한 배열로 만든 큐의 시작과 끝이 이어져있다고 생각하면 된다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

#define QUEUE_CAPACITY 8 // 많이 쓰이므로 미리 정의해놓자

int queue[100];
int head = 0, tail = 0;
int queue_size = 0;

void enqueue(int n)
{
    if (queue_size == 8)
    {
        cout << "queue is full!" << endl;
        return ;
    }
    queue[tail] = n;
    tail = (tail + 1) % QUEUE_CAPACITY; // tail 앞으로 한 칸 이동, 범위를 넘어가면 0으로 회귀
    queue_size++;
    return;
}

int dequeue()
{
    if (queue_size == 0)
    {
        cout << "queue is empty!" << endl;
        return 0;
    }
    int r = queue[head];
    head = (head + 1) % QUEUE_CAPACITY; // head 앞으로 한 칸 이동, 범위를 넘어가면 0으로 회귀
    queue_size--;
    return r;
}

int main()
{
    int input;
    while (true)
    {
        cin >> input;
        if (input == -1)
        {
            break;
        }
        else if (input == 0)
        {
            cout << dequeue() << endl;
        }
        else if (input > 0)
        {
            enqueue(input);
        }
    }
    return 0;
}

결국 원형 큐에서 가장 중요한 것은, 인덱스를 증가시키되, 범위를 초과하면 0으로 회귀시키는 것이다. 그리고 이러한 아이디어는 정확히 나머지 연산자(%)와 부합한다. 이 아이디어는 다양하게 활용되므로, 잘 기억해두자.

1

tail = (tail + 1) % QUEUE_CAPACITY;

1

head = (head + 1) % QUEUE_CAPACITY;

원형 큐에서 head와 tail을 인자로 받고, queue_size를 반환할 수 있는 함수를 짤 수는 없을까? 즉, 우리가 배열을 이용해서 큐를 구현할 때 사용했던 tail - head처럼 말이다. 결론부터 말하자면 조금 어려운 일인 것 같다. 필자는 밑의 코드까지 작성하고 포기했다.

1
2
3
4
5
6
7
8
9
10
11

int queue_size()
{
    if (tail >= head)
   {
       return tail - head;
   }
   else
   {
       return QUEUE_CAPACITY - (head - tail)
   }
}

왜 여기에서 포기하게 되었냐면, 디버깅을 해보니 “데이터가 큐에 꽉 찬 상황”과 “큐가 비어있는 상황”을 구분할 수 없었기 때문이다. 두 가지 상황 모두 head == tail 조건을 만족시킨다. (만약 책의 코드를 따랐다면, head = tail + 1 조건을 만족시킬 것이다.) 따라서 생각이 여기까지 도달했을 때, 다시 위로 올라가 int queue_size를 정의하고 enqueue(int n)과 dequeue()에 각각 queue_size++과 queue_size--를 추가했다… ㅠㅠ

우리는 이렇게 원형 큐를 구현할 수 있었고, 이는 기존의 큐가 가진 문제점을 해결할 수 있다.

배열로 스택 작성하기

큐(Queue)는 먼저 들어간 데이터가 나중에 나오는, 즉 마지막에 들어간 데이터가 맨 처음에 나오는 자료구조를 말한다. (선입후출) (그러한 관점에서, 꽤 불공평하다.)

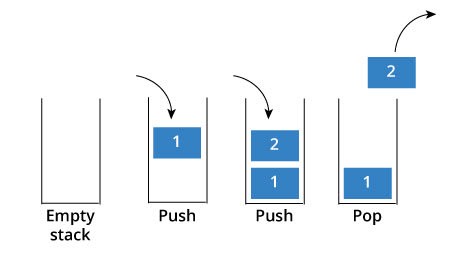stack 스택

스택에 데이터를 넣을 때에는 push라는 용어를 쓰고, 데이터를 뽑아낼 때에는 pop라는 용어를 쓴다.

배열로 큐를 구현했을 때와 마찬가지로, 인덱스를 변수로 놓는 것이 구현의 첫 걸음이다. 넣는 인덱스와 뽑는 인덱스가 동일하므로, 이들을 변수 top으로 놓자.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

int stack[100];
int top = 0; // top은 데이터가 들어왔을 때 놓을 인덱스로 놓자

void push(int n)
{
    if (top == 8)
    {
        cout << "queue is full!" << endl;
        return ;
    }
    stack[top] = n;
    top++;
    return;
}

int pop()
{
    if (top == 0)
    {
        cout << "queue is empty!" << endl;
        return 0;
    }
    int r = stack[top - 1];
    top--;
    return r;
}

int main()
{
    int input;
    while (true)
    {
        cin >> input;
        if (input == -1)
        {
            break;
        }
        else if (input == 0)
        {
            cout << pop() << endl;
        }
        else if (input > 0)
        {
            push(input);
        }
    }
    return 0;
}

요런 식으로 구현할 수 있다. (큐보다 훨씬 쉽다.)

위 경우 스택의 크기는 top이라는 General한 방법으로 구할 수 있다.

쉽기야 하지만, 한 가지 고려해야할 것은 인덱스 변수 top이 “push(n)할 때 입력된 데이터가 들어갈 자리의 인덱스”인지 “pop()할 때 뽑힐 데이터의 인덱스”인지 구분하는 것이다. 위 코드의 경우 전자를 따랐다.

일반적인 데이터 타입을 다룰 수 있는 (원형) 큐 작성하기

캬… 어려운 거 나왔다.

C언어에서 일반적인 데이터 타입을 다룰 수 있는 방법은 무엇일까? C언어에서 모든 데이터 타입의 변수를 다룰 수 있는 방법은 없지만, 모든 데이터 타입의 포인터를 저장할 수는 있다. 그것은 바로 void *이다. void *는 데이터의 주소값(포인터)을 대입할 수 있는데, 대입하거나 대입될 때 자동으로 형 변환이 일어난다.

1

int* x = ptr; // ptr <- void* 타입

따라서 타입 코드만 조금 수정하면 될 것 같다.

ㅋㅋㅋ 방금 해보고 왔는데 안된다. C++에서는 기본적으로 void*를 임의의 다른 포인터형으로 자동 변환해주지 않는다. 수동으로 형변환을 해줘야 한다. (자동 변환해주는 거는 C에서의 이야기이다. 이러한 차이는 C++과 C의 미세한 차이에 속한다.)

1

int* x = (int *)ptr; // ptr <- void* 타입

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

#define QUEUE_CAPACITY 8

void* queue[100]; // 큐의 원소는 각 값의 포인터
int head = 0, tail = 0;
int queue_size = 0;

void enqueue(void* n) // enqueue시 인자는 값의 포인터
{
    if (queue_size == 8)
    {
        cout << "queue is full!" << endl;
        return ;
    }
    queue[tail] = n;
    tail = (tail + 1) % QUEUE_CAPACITY;
    queue_size++;
    return;
}

void* dequeue() // 반환 값은 포인터 형식이므로 void*
{
    if (queue_size == 0)
    {
        cout << "queue is empty!" << endl;
        return nullptr;
    }
    void* r = queue[head]; // 반환 값은 포인터 형식이므로 void*
    head = (head + 1) % QUEUE_CAPACITY;
    queue_size--;
    return r;
}

사실 여기까지 적었지만, 필자는 main()을 어떻게 적어야 할지 잘 모르겠다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

int main()
{
    int input;
    while (true)
    {
        cin >> input;
        if (input == -1)
        {
            break;
        }
        else if (input == 0)
        {
            int *r = (int*)(dequeue());
            cout << *r << endl;
        }
        else if (input > 0)
        {
            int x = input; // 여기서 문제가 생긴듯
            enqueue(&x);
        }
    }
    return 0;
}

여기까지 적었는데, 문제가 있다. 실행해보면 dequeue를 호출할 때마다 동일한 값만 나온다. 그리고 이것은 아마도 11번째 행 else if (input > 0)영역이 문제인 것 같은데, 내가 기대했던 것은 매번 저 영역을 지날 때마다 int x를 실행하여 이름은 x로 똑같지만 포인터 값이 항상 다른 변수를 만드는 것이었지만, 실행해보니 항상 똑같은 값이 들어가는 모양이다. (실제로 배열의 내부를 확인해보니 그렇더라) 이를 해결할 수 있는 다른 멋진 방법이 필요해보인다.

다음에 이 글을 보면 해결할 수 있기를!

연결 리스트

우리는 위에서 배열로 큐를 구현하는 것의 문제점과 한계를 직면했고, 그에 대한 해결책으로 원형 큐를 배웠다. 하지만, 해결책은 원형 큐만이 있는 것은 아니다. 우리가 배울 기법은 이 문제의 해결책이 되는데, 그것은 바로 연결 리스트이다.

연결 리스트의 노드는 key 변수와 다음 노드를 가리키는 포인터 struct _node *next로 이루어져 있다. (포인터의 형은 구현 방식에 따라 차이가 있지만, 책에서는 struct 타입으로 구현하였다.) head는 첫번째 노드를 가리키고, tail은 마지막 노드를 가리킨다. 그리고 노드 tail의 포인터 값은 아무것도 가리키지 않기에, NULL을 가진다. (아래 그림을 보면 이해가 쉬울 것이다)

장점
연결리스트는 배열과 다르게 중간에 노드를 삽입하거나 제거할 때 원소를 밀어내거나 이동시킬 필요가 없다. 그냥 연결을 끊고 새로운 노드와 붙이거나, 한 노드의 양 연결을 끊고 이 노드를 배재시킨 후 연결시키면 끝나기 때문이다.
단점
그러나 임의의 위치에 있는 (i번째) 원소를 찾는 과정이 오래 걸린다. 완전 탐색을 수행하기 때문.

연결리스트의 종류로는 이중 연결 리스트 (Doubly Linked List), 원형 연결 리스트 (Circular Linked List) 등이 있는데, 요 책에서는 단일 연결 리스트(Singular Linked List)만 다룬다.

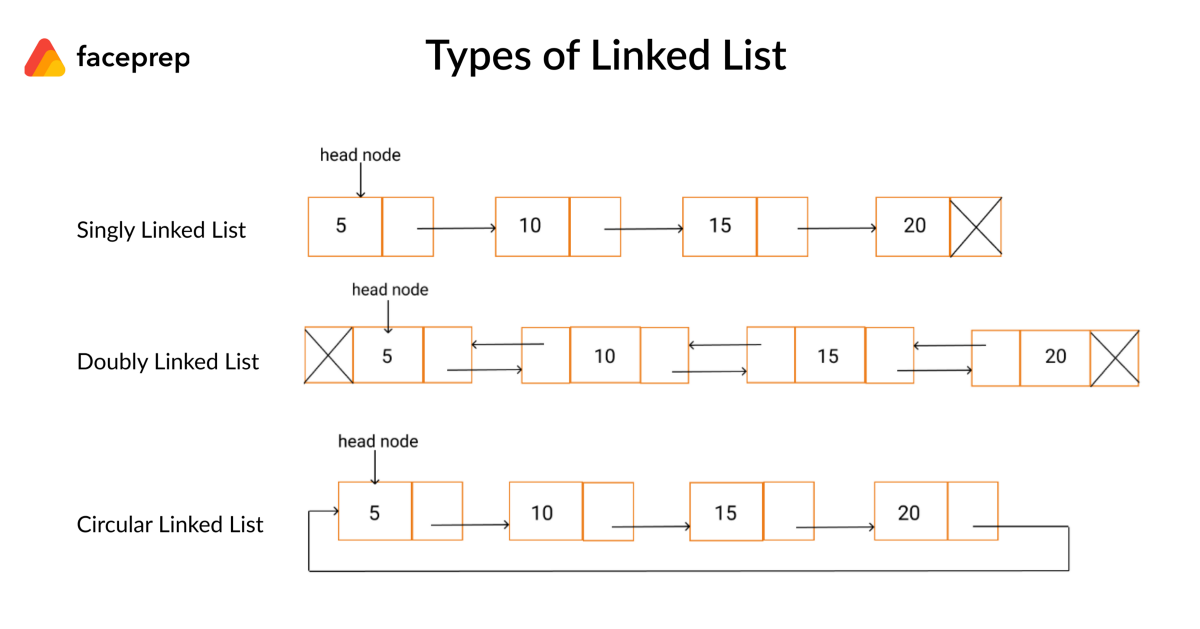linked list 연결 리스트

연결 리스트로 큐 작성하기

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

struct _node
{
    int key;
    struct _node *next;
};

typedef struct _node node_t;

node_t *head = NULL, *tail = NULL; // head와 tail은 첫 노드와 마지막 노드를 가리키는 포인터, 초기는 NULL

void insert_node(int n) // 숫자 n을 리스트에 추가할 것
{
    node_t *new_node = (node_t*)malloc(sizeof(node_t));
    new_node->key = n;
    new_node->next = NULL; // 추가된 노드가 가리켜야할 노드는? 아무것도 가리키지 않으므로 NULL!
    if (head == NULL) // head가 NULL이라면, 즉 지금 들어온 노드가 첫 번째 입력이라면
    {
        head = new_node;
        tail = new_node;
    }
    else
    {
        tail->next = new_node;
        tail = new_node;
    }
}

int delete_node()
{
    node_t *node; // 출력 노드의 포인터
    int r;
    if (head == NULL) // 지금 리스트가 비어있다면
        return -1;
    node = head; // 출력 노드 = head
    head = head->next; // head 노드는 출력되므로(사라지므로), head 노드는 그 다음 노드로 업데이트 됨
    if (head == NULL) // 다음 노드가 NULL이라면, 즉 위에서 뽑았던 노드가 마지막 노드였다면
        tail = NULL; // 리스트가 텅 빈 것이므로 tail을 NULL로 바꾸기
    r = node->key;
    free(node);
    return r;
}

int main()
{
    int input;
    while (true)
    {
        cin >> input;
        if (input == -1)
        {
            break;
        }
        else if (input == 0)
        {
            cout << delete_node() << endl;
        }
        else if (input > 0)
        {
            insert_node(input);
        }
    }
    return 0;
}

연결 리스트 구현에 있어 몇 가지 유의해야하는 점들이 있다.

구조체(struct)에 대하여 구조체란 여러 변수들의 묶음으로 이해하면 편하다. 그리고 여러 변수들을 묶었기에, 이 구조체를 새로운 타입으로써 바라볼 수 있다.

  • 구조체 선언: 구조체 _node는 정수형 변수 key와 구조체 _node의 포인터 변수 next의 묶음이다.
    1
2
3
4
5

    struct _node
{
  int key;
  struct _node *next;
};
  • 구조체를 간지나게 쓰기: struct _node *node보다는 node_t *node가 더 간결하고 간지난다. 따라서 typedef를 통해서 구조체의 이름을 새로운 타입으로 정의하자.
    1

    typedef struct _node node_t; // struct _node는 node_t
  • 구조체의 값 접근: 구조체 자체가 주어졌는지, 구조체의 포인터가 주어졌는지에 따라 다르다. 차이를 잘 기억해놓자.
    1
2
3
4
5
6
7
8

    // 구조체가 주어짐
struct A a;
a.x = 1;
a.y = 2; // 요런 . 연산자로 접근
// 구조체의 포인터가 주어짐
struct A *a;
a->x = 1;
a->y = 2; // 요런 -> 연산자로 접근

head와 tail은 위 배열에서 보았던 방법과 같이 인덱스로 사용된 것이 아니고 포인터로 사용된다. 따라서 리스트가 빈 상황에서 꼭 아래와 같이 NULL로 초기화를 시켜주어야 한다. 그리고 리스트가 빈 상황은 delete_node() 안에서 head의 값을 업데이트할 때 head의 다음 노드를 가리키는 포인터가 NULL 인 것으로 알 수 있다.

1
2
3
4
5

head = head->next; // head 노드는 출력되므로(사라지므로), head 노드는 그 다음 노드로 업데이트 됨
if (head == NULL) // 다음 노드가 NULL이라면, 즉 위에서 뽑았던 노드가 마지막 노드였다면
{
    tail = NULL; // 리스트가 텅 빈 것이므로 tail을 NULL로 바꾸기
}

이 연결 리스트는 대기번호를 몇 개까지 받을 수 있을까?

코드를 작성하여 확인해보자.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

int main()
{
    double cnt = 0;
    while (true)
    {
        cout << cnt << endl;
        try
        {
            insert_node(1);
        }
        catch(const std::exception& e)
        {
            std::cerr << e.what() << '\n';
            break;
        }
        cnt++;
    }
    return 0;
}

지금 코드를 짜서 실행시키고 있긴 한데… 아직도 안 끝났다 ㅋㅋ 결과 해석은 나중에 써야할 듯.

연결 리스트를 이용하여 양쪽 끝에서 삽입과 삭제가 일어나는 Double Ended Queue 작성하기 (작성 중)

끝에 추가했던 코드를 맨 앞에 추가하는 코드로 수정하면 될 것 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95

struct _node
{
    int key;
    struct _node *next;
};

typedef struct _node node_t;

node_t *head = NULL, *tail = NULL; // head와 tail은 첫 노드와 마지막 노드를 가리키는 포인터, 초기는 NULL

void insert_front_node(int n) // 숫자 n을 리스트에 추가할 것
{
    node_t *new_node = (node_t*)malloc(sizeof(node_t));
    new_node->key = n;
    new_node->next = head; // 추가된 노드가 가리켜야할 노드는? 맨 앞이 되므로 head!
    if (head == NULL) // head가 NULL이라면, 즉 지금 들어온 노드가 첫 번째 입력이라면
    {
        head = new_node;
        tail = new_node;
    }
    else
    {
        head = new_node;
    }
}

// 밑에 놈을 어떻게 적지? 정확히는, tail을 뽑고 tail을 어떻게 업데이트하지?
int delete_front_node()
{
    node_t *node; // 출력 노드의 포인터
    int r;
    if (head == NULL) // 지금 리스트가 비어있다면
        return -1;
    node = head; // 출력 노드 = head
    head = head->next; // head 노드는 출력되므로(사라지므로), head 노드는 그 다음 노드로 업데이트 됨
    if (head == NULL) // 다음 노드가 NULL이라면, 즉 위에서 뽑았던 노드가 마지막 노드였다면
        tail = NULL; // 리스트가 텅 빈 것이므로 tail을 NULL로 바꾸기
    r = node->key;
    free(node);
    return r;
}

void insert_node(int n) // 숫자 n을 리스트에 추가할 것
{
    node_t *new_node = (node_t*)malloc(sizeof(node_t));
    new_node->key = n;
    new_node->next = NULL; // 추가된 노드가 가리켜야할 노드는? 아무것도 가리키지 않으므로 NULL!
    if (head == NULL) // head가 NULL이라면, 즉 지금 들어온 노드가 첫 번째 입력이라면
    {
        head = new_node;
        tail = new_node;
    }
    else
    {
        tail->next = new_node;
        tail = new_node;
    }
}

int delete_node()
{
    node_t *node; // 출력 노드의 포인터
    int r;
    if (head == NULL) // 지금 리스트가 비어있다면
        return -1;
    node = head; // 출력 노드 = head
    head = head->next; // head 노드는 출력되므로(사라지므로), head 노드는 그 다음 노드로 업데이트 됨
    if (head == NULL) // 다음 노드가 NULL이라면, 즉 위에서 뽑았던 노드가 마지막 노드였다면
        tail = NULL; // 리스트가 텅 빈 것이므로 tail을 NULL로 바꾸기
    r = node->key;
    free(node);
    return r;
}

int main()
{
    int input;
    while (true)
    {
        cin >> input;
        if (input == -1)
        {
            break;
        }
        else if (input == 0)
        {
            cout << delete_node() << endl;
        }
        else if (input > 0)
        {
            insert_node(input);
        }
    }
    return 0;
}

오늘은 여기까지! (2022/4/3 16시)

Problem Solving, 문제로 풀어보는 알고리즘
ps book
This post is licensed under CC BY 4.0 by the author.
Recently Updated
Trending Tags
c++ c book decs ps dm etc lecture qz
Contents
Trending Tags
c++ c book decs ps dm etc lecture qz